Teaching
2025/2026. National University of Singapore
Advanced Probability (MA5260)
In this course, after an introduction to the basics of probaility theory with measure theoretic formalism we will go through multiple foundational results such as the Law of Large Number, the Central Limit Theorem, the study of Large Deviations, Martingales, Markov Chains, Brownian Motion to name a few.
Stochastic Processes I (MA3238S)
In this course we will study discrete stochastic processes: random walks, martingales, Markov chains, graphs and more.
2024/2025. National University of Singapore
Advanced Probability (MA5260)
In this course, after an introduction to the basics of probaility theory with measure theoretic formalism we will go through multiple foundational results such as the Law of Large Number, the Central Limit Theorem, the study of Large Deviations, Martingales, Markov Chains, Brownian Motion to name a few.
Stochastic Processes and Algorithms (MA5249)
This graduate level course explores stochastic processes and their applications in algorithms. Topics include: Brownian motion and its properties, diffusion limits of random walks and Donsker’s invariance (statement only) , Ito integrals, Ito formula and Martingale Representation, Stochastic differential equations, Filtering, Diffusions, Feynman Kac formula, Girsanov theorem, Fokker-Planck equation, stationary Gaussian processes, Random fields (Gaussian and Markov) and Gibbs distributions, Markov Chain Monte Carlo, Hidden Markov models, Stochastic Gradient Descent, basics of stochastic approximation.
2023/2024. University of Warwick, Department of Statistics
Multivariate Statistics (ST323)
In this course I covered the basics of Multivariate Statistics, from Principal Component Analysis, to Classification and Clustering. This course included advanced topics, which covered basic results in Random Matrix Theory.
2022/2023. University of Warwick, Department of Mathematics
Partial Differential Equations (MA3G1)
In this course I covered the basics of PDEs, studying and solving in some special cases the transport equation, the Poisson equation, the heat equation and the wave equation.
Reading Groups
Airy Line Ensemble (2025/2026)
-
Introduction: Gibbs measures on line ensembles, Brownian Gibbs property and statement of strong characterization of the parabolic Airy Line ensemble.
Notes

A sample of the ice model. 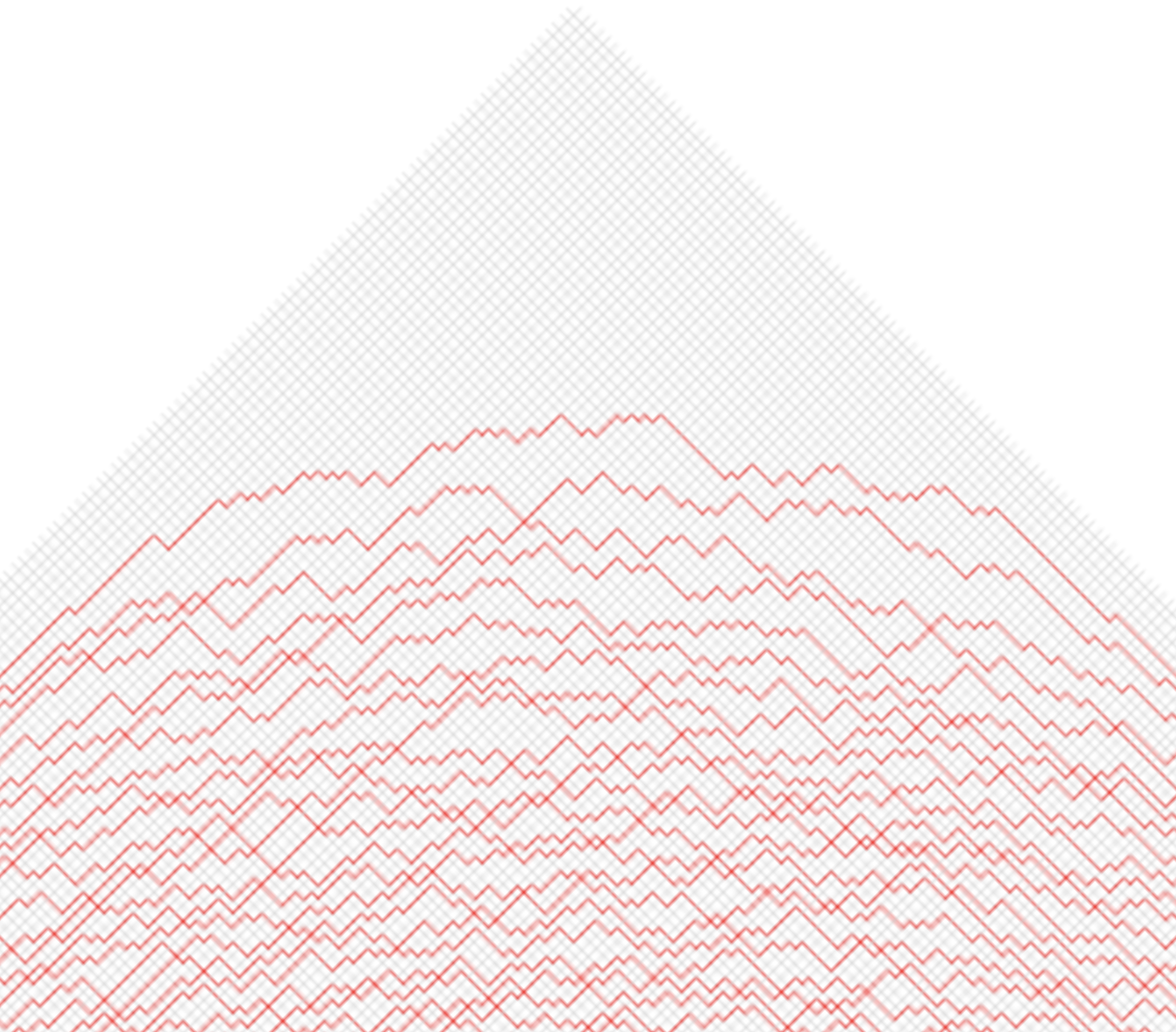
A close up on the frozen-liquid interface. -
The Gaussian Unitary Ensemble (GUE): the Ginibre formula for eigenvalue distribution, Hermite kernel, semicircle law and Airy point process.
Notes (by Akshay Hegde)
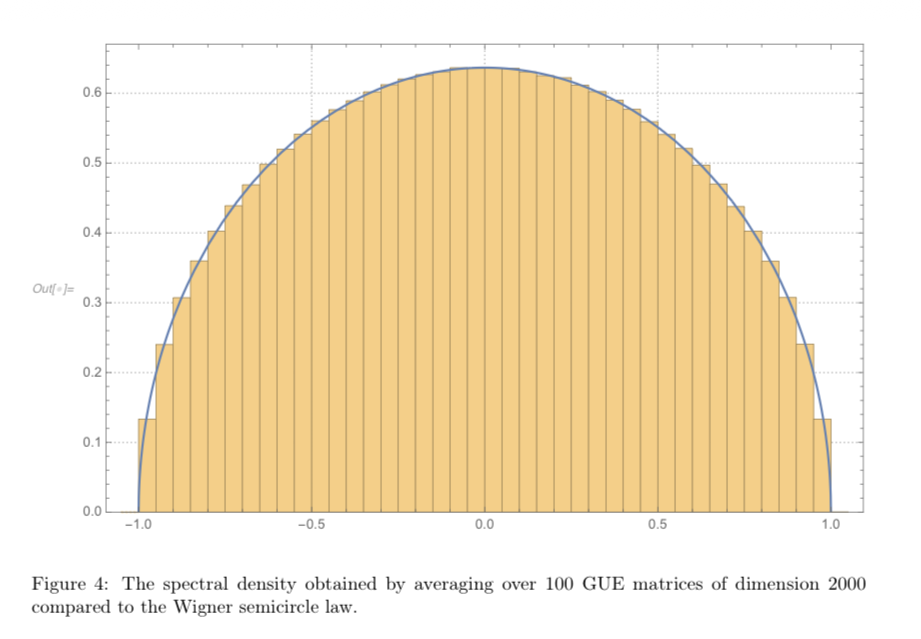
A screenshot from "Random Matrix Theory" by J. Keating and L.P. Arguin representing the semicircle law. -
Dyson's Brownian motion: definition
Notes
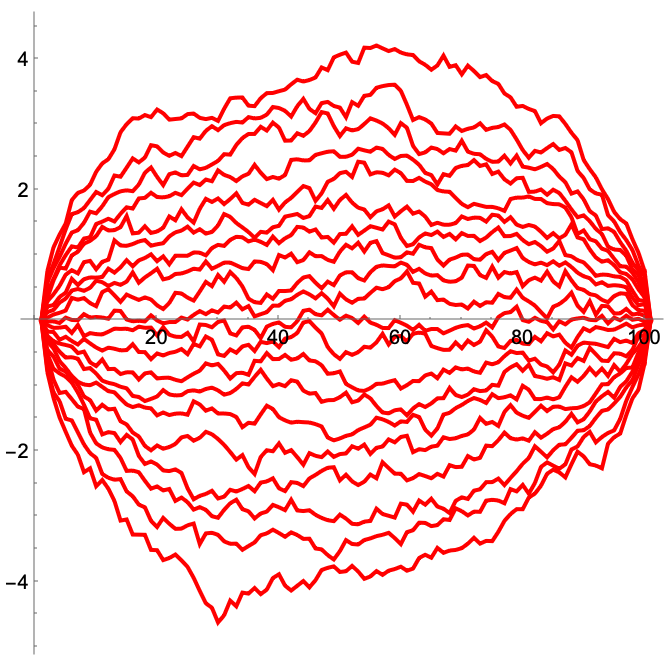
A sample of a Dyson's Brownian bridge.