Research
Papers
Multiplicative Averages of Plancherel Random Partitions: Elliptic Functions, Phase Transitions, and Applications
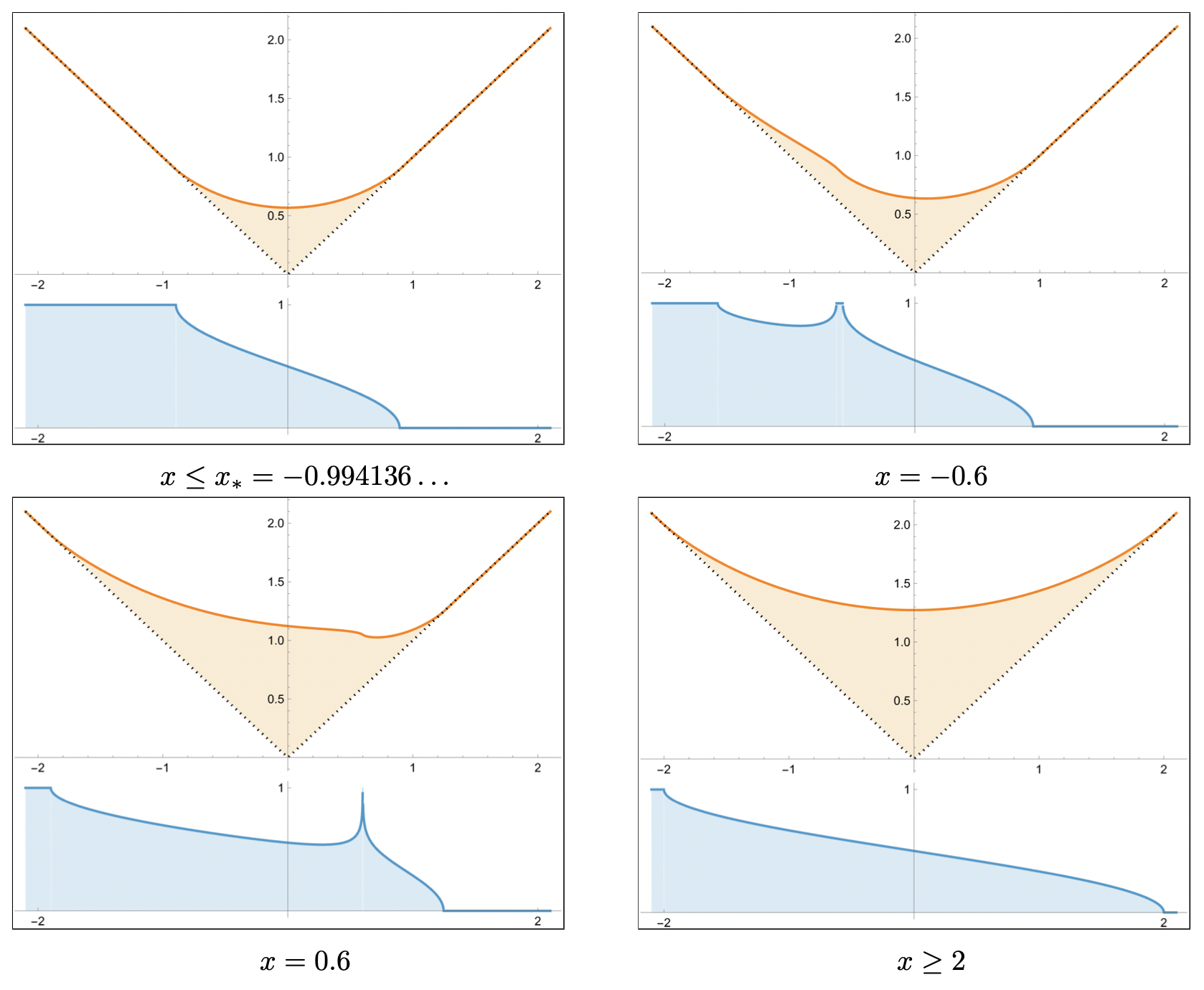
We consider random integer partitions $\lambda$ that follow the Poissonized Plancherel measure of parameter $t^2$. Using Riemann--Hilbert techniques, we establish the asymptotics of the multiplicative averages $$ Q(t,s)=\mathbb{E} \left[ \prod_{i\geq 1} \left(1+ e^{\eta(\lambda_i-i+\frac{1}{2}-s)}\right)^{-1} \right] $$ for fixed $\eta>0$ in the regime $t \to +\infty$ and $s/t=O(1)$. We compute the large-$t$ expansion of $\log Q(t,xt)$ expressing the rate function $\mathcal{F}(x)=− \lim_{t \to \infty} \frac{\log Q(t,xt)}{t^2}$ and the subsequent divergent and oscillatory contributions explicitly in terms of elliptic theta functions. The associated equilibrium measure presents, in general, nontrivial saturated regions and it undergoes two third-order phase transitions of different nature which we describe. Applications of our results include an explicit characterization of tail probabilities of the height function of the $q$-deformed polynuclear growth model and of the edge of the positive-temperature discrete Bessel process and asymptotics of radially symmetric solutions to the 2D Toda equation with step-like shock initial data.
Orthogonality of spin q-Whittaker polynomials
The inhomogeneous spin $q$-Whittaker polynomials are a family of symmetric polynomials which generalize the Macdonald polynomials at $t=0$. In this paper we prove that they are orthogonal with respect to a variant of the Sklyanin measure on the n dimensional torus and as a result they form a basis of the space of symmetric polynomials in n variables. Instrumental to the proof are inhomogeneous eigenrelations, which partially generalize those of Macdonald polynomials. We also consider several special cases of the inhomogeneous spin $q$-Whittaker polynomials, which include variants of symmetric Grothendieck polynomials or spin Whittaker functions.
Lower tail large deviations of the stochastic six vertex model
International Mathematics Research Notice
In this paper, we study lower tail probabilities of the height function $\mathfrak{h}(M,N)$ of the stochastic six-vertex model. We introduce a novel combinatorial approach to demonstrate that the tail probabilities $\mathbb{P}(\mathfrak{h}(M,N) \ge r)$ are log-concave in a certain weak sense. We prove further that for each $\alpha > 0$ the lower tail of $−\mathfrak{h}(\lfloor \alpha N \rfloor,N)$ satisfies a Large Deviation Principle (LDP) with speed $N^2$ and a rate function $ \Phi^{(-)}_\alpha $, which is given by the infimal deconvolution between a certain energy integral and a parabola. Our analysis begins with a distributional identity from [BO17] [arXiv:1608.01564], which relates the lower tail of the height function, after a random shift, with a multiplicative functional of the Schur measure. Tools from potential theory allow us to extract the LDP for the shifted height function. We then use our weak log-concavity result, along with a deconvolution scheme from our earlier paper [arXiv:2307.01179], to convert the LDP for the shifted height function to the LDP for the stochastic six-vertex model height function.
The Symplectic Schur Process
We define a measure on tuples of partitions, called the symplectic Schur process, that should be regarded as the right analogue of the Schur process of Okounkov-Reshetikhin for the Cartan type C. The weights of our measure include factors that are universal symplectic characters, as well as a novel family of "Down-Up Schur functions" that we define and for which we prove new identities of Cauchy-Littlewood-type. Our main structural result is that the point process corresponding to the symplectic Schur process is determinantal and we find an explicit correlation kernel. We also present dynamics that preserve the family of symplectic Schur processes and explore an alternative sampling scheme, based on the Berele insertion algorithm, in a special case. Finally, we study the asymptotics of the Berele insertion process and find explicit formulas for the limit shape and fluctuations near the bulk and the edge. One of the limit regimes leads to a new kernel that resembles the symmetric Pearcey kernel.

Large deviations for the $q$-deformed polynuclear growth
In this paper, we study large time large deviations for the height function $\mathfrak{h}(x,t)$ of the $q$-deformed polynuclear growth introduced in [ABW22] [arXiv:2108.06018]. We show that the upper-tail deviations have speed $t$ and derive an explicit formula for the rate function $\Phi_+(\mu)$. On the other hand, we show that the lower-tail deviations have speed $t^2$ and express the corresponding rate function $\Phi_-(\mu)$ in terms of a variational problem. Our analysis relies on distributional identities between the height function 𝔥 and two important measures on the set of integer partitions: the Poissonized Plancherel measure and the cylindric Plancherel measure. Following a scheme developed in [DT21] [arXiv:1910.09271], we analyze a Fredholm determinant representation for the $q$-Laplace transform of $\mathfrak{h}(x,t)$, from which we extract exact Lyapunov exponents and through inversion the upper-tail rate function $\Phi_+$. The proof of the lower-tail large deviation principle is more subtle and requires several novel ideas which combine classical asymptotic results for the Plancherel measure and log-concavity properties of Schur polynomials. Techniques we develop to characterize the lower-tail are rather flexible and have the potential to generalize to other solvable growth models.
Relationships between two linearizations of the box-ball system : Kerov-Kirillov-Reschetikhin bijection and slot configuration
The box-ball system (BBS), which was introduced by Takahashi and Satsuma in 1990, is a soliton cellular automaton. Its dynamics can be linearized by a few methods, among which the best known is the Kerov-Kirillov-Reschetikhin (KKR) bijection using rigged partitions. Recently a new linearization method in terms of “slot configurations” was introduced by Ferrari-Nguyen-Rolla-Wang, but its relations to existing ones have not been clarified. In this paper we investigate this issue and clarify the relation between the two linearizations. For this we introduce a novel way of describing the BBS dynamics using a carrier with seat numbers. We show that the seat number configuration also linearizes the BBS and reveals explicit relations between the KKR bijection and the slot configuration. In addition, by using these explicit relations, we also show that even in case of finite carrier capacity the BBS can be linearized via the slot configuration.
Solvable models in the KPZ class: approach through Periodic and Free Boundary Schur measures
Annals of Probability (to appear)
We explore probabilistic consequences of correspondences between $q$-Whittaker measures and periodic and free boundary Schur measures established by the authors in the recent paper [arXiv:2106.11922]. The result is a comprehensive theory of solvability of stochastic models in the KPZ class where exact formulas descend from mapping to explicit determinantal and pfaffian point processes. We discover new variants of known results as determinantal formulas for the current distribution of the ASEP on the line and new results such as Fredholm pfaffian formulas for the distribution of the point-to-point partition function of the Log Gamma polymer model in half space. In the latter case, scaling limits and asymptotic analysis allow to establish Baik-Rains phase transition for height function of the KPZ equation on the half line at the origin.
Skew RSK dynamics: Greene invariants, affine crystals and applications to $q$-Whittaker polynomials
Iterating the skew RSK correspondence discovered by Sagan and Stanley in the late ’80s, we define a deterministic dynamics on the space of pairs of skew Young tableaux $(P,Q)$. We find that this skew RSK dynamics displays conservation laws which, in the picture of Viennot’s shadow line construction, identify generalizations of Greene invariants. The introduction of a novel realization of 0-th Kashiwara operators reveals that the skew RSK dynamics possesses symmetries induced by an affine bicrystal structure, which, combined with connectedness properties of Demazure crystals, leads to its linearization. Studying asymptotic evolution of the dynamics started from a pair of skew tableaux $(P,Q)$, we discover a new bijection $\Upsilon:(P,Q) \to (V,W;\kappa,\nu)$. Here $(V,W)$ is a pair of vertically strict tableaux, i.e., column strict fillings of Young diagrams with no condition on rows, with shape prescribed by the Greene invariant, $\kappa$ is an array of non-negative weights and $\nu$ is a partition. An application of this construction is the first bijective proof of Cauchy and Littlewood identities involving $q$-Whittaker polynomials. New identities relating sums of $q$-Whittaker and Schur polynomials are also presented.
Identity between restricted Cauchy sums for the $q$-Whittaker and skew Schur polynomials
Symmetry, Integrability and Geometry: Methods and Applications (SIGMA)
The Cauchy identities play an important role in the theory of symmetric functions. It is known that Cauchy sums for the $q$-Whittaker and the skew Schur polynomials produce the same factorized expressions modulo a $q$-Pochhammer symbol. We consider the sums with restrictions on the length of the first rows for labels of both polynomials and prove an identity which relates them. The proof is based on techniques from integrable probability: we rewrite the identity in terms of two probability measures: the $q$-Whittaker measure and the periodic Schur measure. The relation follows by comparing their Fredholm determinant formulas.
Spin $q$-Whittaker polynomials and deformed quantum Toda
Communications in Mathematical Physics
Spin $q$-Whittaker symmetric polynomials labeled by partitions $\lambda$ were recently introduced by Borodin and Wheeler (arXiv:1701.06292) in the context of integrable $\mathfrak{sl}_2$ vertex models. They are a one-parameter deformation of the $t=0$ Macdonald polynomials. We present a new more convenient modification of spin $q$-Whittaker polynomials and find two Macdonald type $q$-difference operators acting diagonally in these polynomials with eigenvalues, respectively, $q^{(-\lambda_1)}$ and $q^{(\lambda_N)}$ (where $\lambda$ is the polynomial’s label). We study probability measures on interlacing arrays based on spin $q$-Whittaker polynomials, and match their observables with known stochastic particle systems such as the $q$-Hahn TASEP. In a scaling limit as $q \to 1$, spin $q$-Whittaker polynomials turn into a new one-parameter deformation of the $\mathfrak{gl}_n$ Whittaker functions. The rescaled Pieri type rule gives rise to a one-parameter deformation of the quantum Toda Hamiltonian. The deformed Hamiltonian acts diagonally on our new spin Whittaker functions. On the stochastic side, as $q \to 1$ we discover a multilevel extension of the beta polymer model of Barraquand and Corwin (arXiv:1503.04117), and relate it to spin Whittaker functions.
Yang-Baxter random field and stochastic vertex models
Bijectivization refines the Yang-Baxter equation into a pair of local Markov moves which randomly update the configuration of the vertex model. Employing this approach, we introduce new Yang-Baxter random fields of Young diagrams based on spin q-Whittaker and spin Hall-Littlewood symmetric functions. We match certain scalar Markovian marginals of these fields with (1) the stochastic six vertex model; (2) the stochastic higher spin six vertex model; and (3) a new vertex model with pushing which generalizes the $q$-Hahn PushTASEP introduced recently by Corwin-Matveev-Petrov (arXiv:1811.06475). Our matchings include models with two-sided stationary initial data, and we obtain Fredholm determinantal expressions for the $q$-Laplace transforms of the height functions of all these models. Moreover, we also discover difference operators acting diagonally on spin q-Whittaker or (stable) spin Hall-Littlewood symmetric functions.
Stationary Higher Spin Six Vertex Model and $q$-Whittaker measure
Probability Theory and Related Fields
In this paper we consider the Higher Spin Six Vertex Model on the lattice $\mathbb{Z}_{\ge 2} \times \mathbb{Z}_{\ge 1}$. We first identify a family of translation invariant measures and subsequently we study the one point distribution of the height function for the model with certain random boundary conditions. Exact formulas we obtain prove to be useful in order to establish the asymptotic of the height distribution in the long space-time limit for the stationary Higher Spin Six Vertex Model. In particular, along the characteristic line we recover Baik-Rains fluctuations with size of characteristic exponent 1/3. We also consider some of the main degenerations of the Higher Spin Six Vertex Model and we adapt our analysis to the relevant cases of the $q$-Hahn particle process and of the Exponential Jump Model.
Proceedings
New approach to KPZ models through free fermions at positive temperature
Journal of Mathematical Physics 64 (8)
We give a short account of our new approach to study models in the Kardar–Parisi–Zhang universality class by connecting them to free fermions at positive temperature. Our ideas and methods are explained mainly for the semi-discrete directed polymer model due to O’Connell and Yor.
Determinantal structures in the $q$-Whittaker measure
JStochastic Analysis, Random Fields and Integrable Probability—Fukuoka 2019
The $q$-Whittaker measure is a probability measure on the set of partitions. We show a Fredholm determinant formula for an expectation value with respect to this measure, which is the $q$-Laplace transform of the marginal distribution on the last element of the partition. Contrary to the typical approaches in integrable probability, our method does not focus on the $q$-moment generating function but explains the origin of its determinantal structure using Ramanujan’s summation formula and the Frobenius determinant. This method can be applied to analyze on the fluctuations in the stationary situations in $q$-TASEP, higher spin exclusion process, and the directed polymer in the beta-distributed random environment.